Abstract
Although a relatively new phenomenon, the game theory holds considerable significance for actors in the international system who have conflicting relationships. This paper will try to analyse the concept, modelling process, and implementation of game theory in IR, with a sole focus on non-cooperative game structures in the area of international security studies. The paper will provide a thorough understanding of the dynamics of game theory in general and its application in IR in specific. This paper attempts to sum-up the various theoretical and structural requirements needed for understanding and analysing the game theory in tandem with international relations.
Keywords: Game Theory, International relations, Actors, Rational, Interactions, Political.
Overview
The field of International Relations (IR) is chalked by broad foundational and structural theories. One of its axioms establishes nation-states as autonomous rational players operating in an anarchic global system characterised by constant interactions and interdependencies. This interconnectedness leads to strategic encounters, which opens up a world of complicated and unintelligible interactions. Despite academics' best efforts to comprehend and extrapolate these associational complexities, scholars find it difficult to keep track of the event-shaping decisions due to the sheer volume of actors and choices. Furthermore, it is obvious from current academic international relations (IR) research that advanced methods of analysis are rarely used to understand strategic relationships. The most significant exceptions to this flaw are rational choice theory and its most essential component, game theory.
While the rational choice approach refers to any method - that assumes political actors make rational decisions and base their political analysis on those assumptions. We have a full toolkit in game theory that allows us to investigate such interactions in depth. Given the actors' basic preferences and strategic environment, we may deduce how they rank the various policies available to them, as well as the probable outcome(s) of their policy choices. Game theory is most commonly used in international relations literature to model general political processes such as crisis bargaining, alliance formation, and war. Although a relatively new phenomenon (as it emerged in the 20th century), the game theory holds considerable significance for actors in the international system who have conflicting relationships.
In conjunction with the above assertion, Bueno de Mesquita in 2002 advanced five overarching parameters that helped the IR academics to fully grasp the advantages of utilising game theory in international relations(2). Game theory and modelling provide necessary frameworks: in order for motivations, which lie behind the behaviours, to be understood; for explaining strategic interactions; to the ability of formal theory to unite different approaches and theories; for cumulative knowledge accumulation; for the development of methodological understanding in the examination of decision- making mechanisms.
Additionally, due to its primary assumption of international anarchy, game theory in IR also illuminates the implications of varied arrangements of national interests and political circumstances for international conflict and cooperation(3).
As such, there are various game models that mark the ‘IR’ space, for instance, the Chicken Game, the Prisoner’s Dilemma, the Bargaining and War Model, etc, some of which will be covered in this paper. Despite the diversity of these models, there are certain common factors that help us structure game-theoretic models to compose modelling typologies. These comprise the number and conduct of the players that is deduced from the game's inferential structure; the number of probable choices for the different players; considerations on the nature of rationality; and the deficiency of knowledge and information conditions.
Lastly, the use of Game theory (a subset of Rational Choice) as an analytical tool to the study of IR stemmed from the econometric, "positive theory" approach to economics. The predictive method in IR draws on both the legacy of deductive reasoning in economics and the behavioural revolution's empiricist principles(4). It differs from classical behaviourism in that it uses deductive reasoning as a tool for producing hypotheses based on the premise of actor rationality. But this approach is also plagued by certain intrinsic issues. Therefore, it becomes essential to understand the interpretive and theoretical basis of the approach and its lucane in order to encash its optimal utility. This will also be discussed in detail as we move towards the end of this paper, thus, delivering a holistic understanding of the concept and its application.
This paper attempts to sum-up the various theoretical and structural requirements needed for understanding and analysing the game theory in tandem with international relations. Focus is placed just on a prelim and functional understanding of game-theoretic modelling without indulging in complex, multiple-N-person structures. Subsequently, the examination of game theory is also limited to international security studies, leaving a vast chunk of the domain to be explored. Besides, a cursory study of the game theories’ incumbent limitations closes the case of this examination and preempts that when game theory is utilised to develop new insights and understandings rather than to reconstruct specific circumstances, it reaches its full potential for both empirical and theoretical goals. This goal necessitates interpreting game theory as an international politics theory based on nations' goal-seeking behaviour in an interconnected international system. It follows that game models will be useless in forecasting outcomes that are mostly driven by ad hoc or ad hoc action. If such considerations decide all or most situations, the game theory will have little to say about international politics. However, if the underlying premise of self-interested behaviour by strategically rational states is right, and preferences, tactics, and payoffs can be effectively described, the theory will provide significant results.
To begin with, let’s look at what game theory is and what are its underlying conceptual frameworks.
Conceptual Underpinnings
Game Theory
It was during the first part of the twentieth century that the primary examples of mathematical models analysing conflict and collaboration appeared in Europe. When the Theory of Games and Economic Behaviour got published in 1944, some saw it as the definitive theory of all conflictual and competitive decision-making in economics, politics, and international relations (IR). Although much of the Game Theory has been predicated on Von Neumann's concept of "strategy"(5), the application of Game Theory in International Relations is most commonly associated with Thomas Schelling and his 1960 book, The Strategy of Conflict. Schelling is the originator of the Chicken Game and Prisoner's Dilemma, both of which are widely employed today in the field of international security studies.
In contemporary times game theory is considered as a branch of applied mathematics that designs situations in which payoffs emerge from strategic interactions between players. It is a flexible and effective methodological instrument that can be applied to political analysis in a variety of ways. Also, it is quite helpful for developing broad ideas of political relations and can also be employed as a normative tool to compare and contrast conflicting policy prescriptions, or as an empirical tool to organise detailed case studies. Moreover, Game Theory's focus on bureaucracy and decision-making procedures aids our understanding of strategic factors in international relations, allowing us to develop mutual interaction models(6).
Dynamics
A game is any circumstance in which at least two decision-makers engage. Game theory posits that each player has a genuine utility that remains constant during the game. Besides, it is believed that each player is aware of its own usefulness, as well as that of all other players. (Even if the other players' utility functions are unknown, they are least stable.) Since no actor has complete control over events, each must consider the activities of the others. Assume that the best course of action for actor 1 is determined by what actor 2 does, and vice versa. If both comprehend this, 1 will strive to predict and influence 2's decisions, knowing that 2 is doing the same in reverse.
Even if 1 and 2 never meet, their selections will interact, and they will end up with an outcome that is contingent on both of their choices. Mutual threats, deception, bluffing, and counter-bluffing are common in such settings. There are nearly always some shared interests so joint benefits may be realised by cooperating or at the very least by limiting conflict to a minimum. Here, it is asserted that in terms of reciprocal, interrelated decisions, interactions are strategic. The strategic structure is related to the notion that some decisions or actions lead to better or worse outcomes.
Unveiling the inner dynamics, one finds that one of game theory's most appealing propositions is ‘strategic rationality’. Game theory provides for autonomy in state choice while predicting and explaining those choices deterministically via knowledge of the entire strategic interplay. Thus, putting the rational choice of state policy at the Centre of the explanation. As a result, the game model combines intentional actions with a definition of the international political system that constrains that behaviour. It establishes a relationship between systematic macro-theory and voluntaristic decisions. Also central to the game theory is the notion of ‘equilibrium’. This is when each actor chooses the optimum strategy for all situations, assuming that all others behave similarly. The participants in game theory are considered to evaluate (subjectively) the utility/value of each possible result and to make choices that maximise their predicted utility.
Rules, clear results, and interaction are the three main determinants of the game. Besides, conflict, deterrence, negotiations, and collaboration that lead to any deal also constitute a play. In accordance with this notion, the role of game theory in international relations may be defined as a tool that aids in making global political clarifications and assessments while ensuring that our views are disciplined, not disputed, and logically consistent(7).
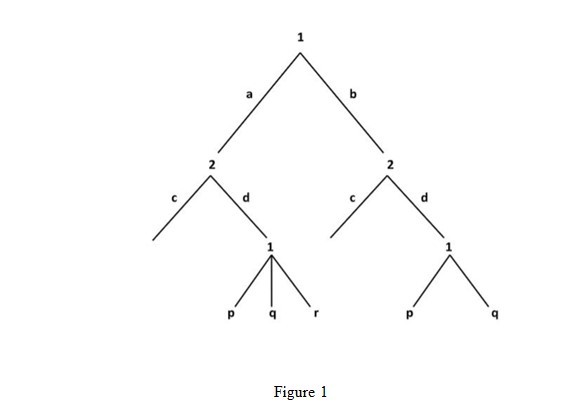
A game can be represented in a variety of ways, the most apparent being as a tree of moves (as illustrated in Figure 1), in which each branch, or move, is controlled by a different player, and the movements available at any one time may be dependent on previous moves. Chess, for example, may be seen as a wonderfully intricate tree of possible moves.
To boot, cooperative (collaborative) and non-cooperative (strategy) game theory are the two primary disciplines of game theory. While in a cooperative game setting, both actors work together to attain a joint goal. The non-cooperative theory is primarily concerned with how intelligent people interact with one another in order to attain their own objectives(8).
The Strokes of Assumptions
The dynamism of game-theoretic modelling stems from its intrinsic assumptions about rationality, utility, equilibria, etc. When applied to the field of IR and security studies five central assumptions become key for successful application. Firstly, the proposition that the rational choice game- theoretic view constitutes social and political outcomes as the aggregate consequence or as the product of choices made by unitary actors is preeminent. Secondly, it is assumed that each actor aims to maximise his or her "subjective prospective utility." Given a certain set of preferences and a fixed number of options, agents will choose the preference that provides the greatest expected payoff. Thirdly, it is held that for every potential play, combinations open to the participants results in a well-defined end-state (victory, loss, or draw) that ends the game, though certain restrictions apply to the specification of actors' preferences: i) an actor's preferences must be full with preferences in order; and (ii) preferences must be transitive (if A is preferred to B and B to C, then A is preferred to C). Further, each end-state is associated with a specific payoff for each player. A zero-sum game, for example, means that the sum of payoffs to all players is zero in each end- state. As a result, building a formal theory necessitates the analyst specifying the structure of the game. This usually entails determining how participants perceive their actions in relation to the probable consequences. Lastly, if the game structure accurately represents the phenomena in consideration and there are no logical errors, the game's equilibria identify the only logically feasible outcomes. These equilibria serve as the foundation for any future empirical assessment of each player's pattern of preferences, information at each option point, and how they perceive their movements to be related to the various outcomes.
Concepts
There remains no doubt that conflict reasoning drives the game-theoretic concepts. It's an amorphous investigation of the mechanism and rationale of social structures and behavioural patterns. Therefore, concepts form the core of game theory and need serious attention. This section will shed light on these central concepts.
Strategy: "A plan of action" is the most common definition of strategy. A strategy, according to J. Friedman, is "A collection of instructions." "A detailed explanation of how a player wants to play a game, from start to finish," as M. Shubik puts it. It is essentially a list of the best options available to each player at each stage of the game. In game theory, a player builds a strategy based on a prediction of his opponent's plan, which provides knowledge about all conceivable tactics, rules, and payoffs, or their possibilities, allowing each player to maximise benefits while avoiding losses. Although strategies can be viewed as simplified representations of more sophisticated decision processes, they are more useful when viewed as simplified representations of general policy positions. The straightforward 2 × 2 game (frequently referred to as "cooperate" and "not cooperate") takes this to its logical endpoint, with only two options. Another context in which strategies can be interpreted is that of "mixed strategies." The mixed strategy of a player is a course of action that is based on private knowledge that is not stated in the model. The player's actions appear to be random, but they are actually predetermined. When we include this information structure in the model, the mixed strategy transforms into a pure strategy in which the action is based on extrinsic data. Besides, dynamic considerations are also included in a strategy by allowing for contingency planning throughout time in response to changing conditions by extending the game (super game).
Pay-offs: The phrase "payoff" or "outcome" refers to what happens at the conclusion of a game in game theory. Furthermore, in IR, the reward might be treaties that define roles and responsibilities, norms for participants to do or not do something collectively, agreements, or money for something or something else that the country players want from their opponent/s. What occurred cannot serve as an explanation for why it happened in an inductive derivation of payoffs. Sen describes the "revealed preference" method as a "strong piece of evasion" since it leads to circular reasoning from actors' decisions back to their preferences(9). For instance, consider international trade in which payoffs are associated with various strategy options, such as tariffs, capital flow limitations, and industry subsidisation. Similarly, military spending provides another example. Theoretical debates regarding the influence of military spending among friends and adversaries, together with knowledge of current international tensions and alliances, can show the underlying strategic structure of these circumstances and possible payoffs(10).
Here it is also important to note that ordinal game models frequently make issues appear symmetric, for example, by treating a very large and a very small state as equal partners in a Prisoners' Dilemma with the "same" ordinal preferences, despite the fact that they are extremely asymmetric when compared to the interpersonal comparison and interval measurement (if, say, the issue of Ukraine-Russia war, which is vital for Ukraine’s national existence but is largely inconsequential for Russia). This concept is essential since many fundamental issues in international politics revolve around considerations of dependency versus reliance.
Nash Equilibrium: Nash Equilibrium is a concept in game theory that predicts the optimal solution in a non-cooperative game. Technically, it is a set of techniques that when used together result in a cell with both payoffs highlighted. A Nash equilibrium happens when all players are concurrently making the best response to each other's strategic choices. Assume that game theory proposes the actions (b#, b*) as a solution to a conflict. Saying (b#, b*) isn't a Nash equilibrium means either b# isn't the best response for player 1, or b* isn't the best response for player 2 or both. On the contrary, a Nash equilibrium is achieved when no one player can get a better result by altering their strategy and all other players' decisions remain consistent. Nash Equilibrium can be further divided into two i.e., pure strategy Nash equilibrium – that has been discussed above and mixed strategy Nash equilibrium – which features that no single participant may get a greater anticipated payoff/utility based on their choice across all strategies and at least one player must use a randomised approach, embarking that no participant can raise his or her projected payoff by using an alternate method.
Lately, there has also been a refinement in the Nash equilibrium to push for a more dynamic equilibrium approach. This refinement is called Sub-game perfect Nash equilibrium or (SPNE). This category of equilibrium is focused on sub-game (parts of the extensive game) and is calculated using the backward induction formula of the subgame. Therefore, it determines a Nash equilibrium in every subgame of the game.
Collectively, strategy-payoffs-equilibrium form the core conceptual bedrock of the game theory as applied in IR. These are wired by the assumption of ‘strategic rationality’ on part of the players, which prompts a calculated and rational, self-centered decision based on their personal preferences and predictions of how others would interact.
Modelling and Constituents
A close correlation between an entity and its model is of much greater significance. A model may be adapted specifically to the subject under consideration since it can be abstract and "built." Its main differentiating features are deductive and internal formal logic (as opposed to analogy's inductive and external logic) as the deductive form of the model aids comprehension and explanation.
A game model can be considered as a straightforward description of a single phenomenon or as incorporating a larger theoretical viewpoint and a more general interpretation of the particular event. As such Game theory creates a healthy tension between both sorts of models and analysing states' motives and how their preferences transfer into payoffs inside a game model is required to be understood from a game-theoretic perspective. For that, scholars have extrapolated three major types of game-theoretic models(11). These are:
● Finite games - generally in matrix form, were the first to appear in political science literature. They range from what O'Neill refers to as proto-garnie theory to Bram’s and Kilgour's more complex formulations(12).
● Repeated games - are concerned with how the spectre of the future influences present judgments. They are most recognized for their work on Tit-for-Tat in the Prisoner's Dilemma, but they are also ideally suited to studying long-term partnerships(13).
● Bayesian games - are concerned with how judgments are influenced by inadequate knowledge about the preferences of one's opponent(s). They have been used successfully in the simulation of global conflicts and nuclear deterrence(14).
In conjunction with these, there are four types of game situations in game-theoretic models that constitute the study of international relations and politics. These are:
➢ Two-player zero-sum game: In this game, the gains of one player equal the losses of the other. The game is not zero-sum if there is even one strategy set for which the sum departs from zero.
➢ Two-player non-zero-sum game: In this type of game, the outcome of the game is split between two participants, and the losses of one player are not always equal to the profits of the other.
➢ N-person zero-sum games: In these games, there are more than two players, the outcome is shared, and the losses of one player are not always equivalent to the profits of another, but the sum eventually becomes zero.
➢ N-person non-zero-sum games: This is another game in which more than two players compete. The scenario is exceedingly complicated in this game, and both sides of the game share the gains and losses to some extent.
Cumulatively, these typologies of approaches bring to fore the modelling frameworks that need to be ascertained if one wants to calibrate an effective game model. There have been various attempts at uniting and simplifying these modelling frameworks and determining the key constituents, amongst them, one of the most prominent attempts has been by Allan and Dupont (1999) where they capture the complexity of the modelling choices in a three-dimensional framework (Figure 2)(15).
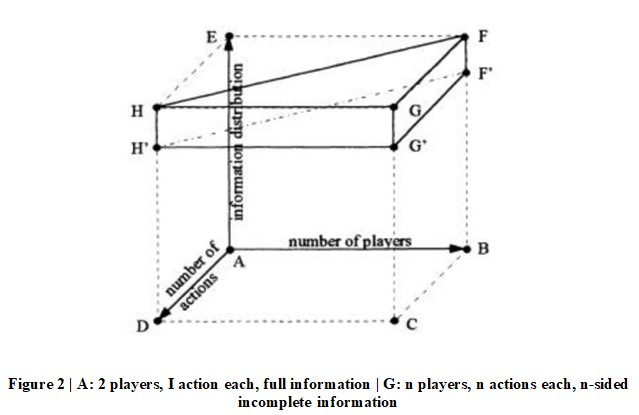
Source: Allan, Pierre, and Cédric Dupont. 1999. "International Relations Theory And Game Theory: Baroque Modelling Choices And Empirical Robustness
From the above diagram, we can specify certain constituents that make up the game and form the basis of the modelling typology:
Players: There would be no strategic engagement if there were fewer than two participants. There is no upper limit: the number of participants can be as high as n, with n signifying infinity (this distinction dates back to Von Neumann). A situation with two participants is the simplest in, and each additional player tends to raise the amount of complexity. The transition from two to three players includes the potential of coalitions, further complicating the strategic calculation and its modelling.
Actions/Choices: One can specify the number of choices available, ranging from one to an unknown number n. A player may have a variable range of options to choose from at each opportunity, or decision node in game-theoretic terms. At each node, at least one alternative between two actions is required, but the number of accessible possibilities is not limited. Bargaining over the amount of a pie is a famous example of this, with each player having an endless number of alternative divisions.
Utility: There are four types of scales recognized by classical measurement theory: "nominal," "ordinal," "linear intervals," and "ratio."16 While zero-sum games appear to suggest a ratio-level assessment of players' utility, their mathematical features are linearly invariant, and they are essentially a subset of constant-sum games. Almost the majority of the work is done on an interval scale.17 Further, in a two-player game, a player's utility may be split down into two parts: the main one based on the player's personal payoff from an outcome, and a contextual one depending on the payoff of the other player. Whether a player's hostility or superiority toward the other player is reflected in the contextual payoff, when the weight assigned on the situational component varies, the game can undergo drastic alterations.
Information Conditions: Information exposure can be broadly divided into two. First is ‘complete information’ that refers to circumstances in which players have complete knowledge of all aspects of the game but may be unaware of past movements. The second is ‘insufficient information’ where players are unaware of some aspects of the interactions. The second term usually describes circumstances in which one or both of the following assumptions are not met. Either the players are aware of their own and other players' tactics or the players are aware of their own and other players' payoff functions. This gives birth to two orders of uncertainty. Uncertainty concerning the above assumptions is referred to as first-order uncertainty while the unpredictability of players' perceptions about first-order uncertainties shapes the second-order uncertainty(18).
Equilibrium Concepts: Sequential equilibria, for example, are more advanced than subgame perfection, which is utilised in circumstances with inadequate knowledge. However, due to the rationality criteria imposed on players in order to choose the best strategy, solution ideas can be distinguished. In this sense, deciding between the initial Nash equilibrium and a slew of improvements made since Nash necessitates varying degrees of reason on the part of participants. Refinements can also be categorised based on the counterfactual reasoning capacity of the hypothetical actors and the consistency standards for information processing. The sequential equilibrium, for example, is a development of the idea of subgame perfection—which is itself a refinement of the Nash equilibrium—that imposes far more explicit limits on the decision-makers’ behaviour.
Contextualising Game Theory in International Relations
The game-theoretical perspective assists us in better understanding the strategic factors in international relations and, as a result, in developing mutual interaction models. It is critical to remember that game theory is a tool, it cannot explain any international issues on its own; it must be applied, otherwise, it is just a series of theorems and proofs. Models simplify complex international interactions, yet queries concerning elements left out of analysis go unanswered(19).
The Realist school of thought in international relations proposes that nation-states are solely motivated by their own national interests and thus are not directed by any ethical-moral consideration. Keeping this in mind, the application of game theory to international relations is based on the premise that states/players can pick any strategy/action based on their preferences, without any restrictions. The interweaving of Game Theory and international relations began with the publication of von Neumann and Morgenstern's seminal work that was oriented towards security and defence challenges, especially the Cold War. Ironically, this initial status still holds the most prominence as, in the field of IR, Game theory is still very much restricted to the analysis of security and defence issues.
Arms Race/Deterrence & Prisoner’s Dilemma
In IR, the case of 2-player direct confrontation where the employment of a deterrence policy when each of them threatens to retaliate for a potential transgression committed by the other as a method of preventing such an offence from occurring in the first place, is a common example. In theory, an offence may include harmful economic policies, armed attacks, and so on. Basically, the majority of deterrence assessments pertain to threats of employing force. The formalisation of the Prisoner’s Dilemma game as an assessment of these above-stated incidents has thus far cherished an important position.
The Prisoner's Dilemma deals with interstate cooperation and problems of joint action. Using the prisoner's dilemma game model helps us understand the contributions of repetitive interactions to cooperation. Here, the liberal contention - ‘self-interest fosters long-term cooperation’, establishes that those actors who do not approach cooperatively or choose to conflict for personal gain, in the short run, can acquire, if they approach close cooperation, more benefits than in the long run. Moreover, this placement of liberal arguments within the Prisoner’s dilemma structure has also helped in its judicious influence on the US’s decisions regarding hydrogen bombs and intercontinental missiles.
Lately, the Prisoner’s Dilemma game model has also been affiliated to another case, i.e., Iran - Saudi Arabia relations. Both the countries share no official communication channel, making it hard to predict each other’s reaction, therefore, resulting in a rising skepticism and antagonism between them. This has led to their incapacity in comprehending each other’s decisions leading to minor skirmishes and thus effectively instigating the prisoner’s dilemma.
Cuban Missile Crisis & Chicken Game
The Chicken Game theory is used to represent scenarios in which international players, in this case, nations, are caught in a conflict in which they have the potential to cause significant harm to one another. In essence, this game mirrors the situation, in which the two parties are on a collision course that might end in disaster. Historical documents, particularly those pertaining to the Cuban Missile Crisis, demonstrated that US decision-makers regarded the game in this light. Figure 3 shows a normal matrix that represents such a model. One side of the matrix displays US and USSR’s alternative strategies: one player controls the rows, while the other controls the columns. This is a finite, two-player non-zero-sum game that has been simplified for a simpler understanding of the Chicken dynamics. Each cell of the matrix represents a possible outcome, and in each cell are the players' preferences. In this case, there are two players labelled "USA" and "USSR"- each having two choices either to "cooperate" or "assert." The figures shown inside the cells represent preference rankings from 1 (worst) to 4 (best) (ordinal preferences). Though the two sides clearly do not have the same preferences, this is not a straightforward zero-sum conflict. If neither side backs down, both end up with their worst possible outcome.

The use of chicken game theory in this framework is an example of conflict and nuclear deterrence in the international relations literature(20).
Other Models
Other than these two core IR Game models, there are certain conflict specific models such as the ‘bargaining and war model’ formed to explore actors’ possible choice of attrition strategies in war, which discovered that despite the costs, states do employ attrition behaviour, which impacts the duration and shape of wars.21 Similarly, an incomplete information model was constituted by Kydd (1997) to show relationships between escalation and fear among states.22 Another pair of predictive modelling and statistical testing was also undertaken by Conrad and Ritter, to make the argument that leaders vulnerable to turnover are less likely to react to international human rights treaties than leaders who are secure in power.23 Maoz (1985) also extends an analysis with a model that studies international relationships beginning at the pre-conflict stage, followed by the initiation of a war, its management, and ending with a study of the conflict termination(24).
Role of Global Environment
The purpose of defining a game structure is to encapsulate the key characteristics of a global scenario. Some are forecasts, while others are assumptions (actors, tactics, and payoffs). Game theory also allows for wider interpretations, thus characteristics that aren't explicitly put into a model can help with understanding and interpretation. The worth of a game simulation is determined by how well it captures important characteristics of the global environment.
The strategic interconnections that each state has with others define the "structural" limits of its options. This view of the ‘structure’ as just the sum of individual units is atomistic, emphasising the structure of specific concerns rather than the structure of the larger international system. As a result, it is insufficient for assessing some world-structure notions. However, the worldwide system is important for establishing the individual game model and drawing inferences from it because of its established patterns of practice and norms. Therefore, the rules of the game model of international politics are divided from the actions of nations within those rules.
Definitely, the established international order influences the definition of issues, players, and options. For instance, the separation of energy issues into the OPEC and IEA (International Energy Agency), recognition of states as relevant decision-makers, and acceptance of restraint from the use of force in resolving energy disputes are all examples of theoretical assumptions about which aspects of the existing trade regime can be taken as "givens" for studying international energy politics. Regimes are not self-contained from the existing global political framework; rather, they are created on top of it and "nested" such that the fabric of one serves as the basis for another.
Incumbent Flaws
There are five key flaws in the game-theoretic model that are perhaps the most serious. First is, the idea that all participants are viewing the same "game" i.e., they agree on what the problem is, who the important parties are, what techniques they employ, and what their preferences are. But this is seldom the case in real life. Here, Harsanyi's (1968) model of games with partial knowledge, models misperceptions by enabling participants to have varying probability estimations of the kind of each other’s types.25 Secondly, rationality’s reference to the effectiveness of the methods ignores the costs and advantages of various methods, and the questions of wisdom. Clearly, how individuals come to have the objectives they have is an essential developmental concern, but it has nothing to do with the instrumental definition of rationality that game theory proposes. Thirdly, there are several Nash equilibria in games. Worse, under certain conditions, practically any game outcome can be sustained as a Nash equilibrium through repeated play. With such a profusion of stable possibilities, a game-theoretic model may not be useful in narrowing down a plethora of accurate predictions to a handful. In actuality, strategies are frequently in flux, and probable outcomes are continually shifting, putting the premise of repeated play of a single-stage game to the test. Additionally, the rules of play proposed by game-theoretic models should represent how players think and act in the strategic scenario being studied. Typical game theory frequently misses the mark based on this reality check, as neither do players choose strategies simultaneously or independently of one another, as assumed in the normal or strategic form of a game that can be represented by a payoff matrix nor do they adhere to a specified sequence of choices, as assumed in the extensive form of a game that can be represented by a game tree(26). Finally, real players don't try to figure out what they should do at the start of a game by working backward from the endpoints of a game tree with numerous levels and branches. Rather, it appears that players build generalisations to make this process easier and have discovered reasonable approximations to backward induction.
Conclusion
In the field of international relations, game theory is a relatively young concept and is critical for the actors in the international system who have conflicting relationships. It has a unique place in understanding IR from a distinct and more straightforward standpoint. As long as the relationships are obvious and appropriate to deal with, the game theory may explain the process, inputs and outputs, potential effects, and future estimation of conflicts.
This paper attempts to sum-up the various theoretical and structural requirements needed for understanding and analysing the game theory in tandem with international relations. Focus is placed just on a prelim and functional understanding of game-theoretic modelling without indulging in complex, multiple-N-person structures. Subsequently, the examination of game theory is also limited to international security studies, leaving a vast chunk of the domain to be explored. Besides, a cursory study of the game theories’ incumbent limitations closes the case of this examination and preempts that when game theory is utilised to develop new insights and understandings rather than to reconstruct specific circumstances, it reaches its full potential for both empirical and theoretical goals. This goal necessitates interpreting game theory as an international politics theory based on nations' goal-seeking behaviour in an interconnected international system. It follows that game models will be useless in forecasting outcomes that are mostly driven by ad hoc or ad hoc action. If such considerations decide all or most situations, the game theory will have little to say about international politics. However, if the underlying premise of self-interested behaviour by strategically rational states is right, and preferences, tactics, and payoffs can be effectively described, the theory will provide significant results.
Further, it can be stated that the obstacle facing the successful empirical application of game theory is establishing this link between an issue area and its game model. To accomplish so, we must provide national goals that are based on both internal and exterior values, bringing various factual and theoretical understandings of international challenges into the approach. The greatest potential of games for understanding international relations is as a theory of state behaviour. Game theory, as a general theory, unites the opposing "interdependence" and "Realist" perspectives in a single framework. While it is constrained by the validity of its assumptions about strategic rationality, game theory is sufficiently adaptable to integrate a wide range of assumptions regarding global politics and individual issues. Overall, game theory only achieves two goals: It constructs models on the basis of intuition and employs logical reasoning based on mathematical knowledge while revealing that deductive reasoning cannot be utilised to find worldly facts on its own.
Declaration: The paper is the original work of the author and has not been published or submitted for publication anywhere else.
End Notes
1 Quackenbush, Stephen L. and Zagare, Frank C. 2006. “Game Theory: Modelling Interstate Conflict.” Sterling. Folker. Jennifer (ed.). Making Sense of International Relations Theory. Boulder. Lynne Rienner. pp. 98–114
2 Bueno de Mesquita. 2002. Accomplishments and Limitations of a Game-Theoretic Approach to International Relations
3 Snidal, Duncan. 1985. "The Game Theory of International Politics". World Politics 38 (1): 25-57.
4 Friedman, Jeffrey. 1996. Introduction: Economic Approaches to Politics. In The Rational Choice Controversy. New Haven: Yale
5 A strategy, in technical terms, is a full formula of activities that specifies what should be done in every potential scenario.
6 Graham Allison's Conceptual Models of the Cuban Missile Crisis, published in 1969, is the most important research on this topic
7 Powell, Robert. 1999. In The Shadow Of Power.
8 This paper delves into the dynamics of the latter – non-cooperative game theory
9 Amartya Sen, "Rational Fools: A Critique of the Behavioural Foundations of Economic Theory," in Hahn and Hollis (fn. I7), 92;emphasis in original
10 Olson, Mancur, and Richard Zeckhauser. 1966. "An Economic Theory Of Alliances". The Review Of Economics and Statistics 48 (3): 266. doi:10.2307/1927082.
11 Referring to noncooperative models with individualistic actors.
12 O'Neill. Steven J. Brams and D. Marc Kilgour. 1988. Game Theory and National Security. New York Basil Blackwell
13 Robert, Axelrod. 1984. The Evolution of Cooperation. New York: Basic Books
14 Mor, Ben D. 1992. "Nuclear Deterrence Theory: The Search For Credibility. By Robert Powell. Cambridge: Cambridge University Press, 1990. 230P. $47.50.". American Political Science Review 86 (1): 293-294. doi:10.2307/1964119.
15 Allan, Pierre, and Cédric Dupont. 1999. "International Relations Theory And Game Theory: Baroque Modelling Choices And Empirical Robustness". International Political Science Review 20 (1): 23-47. doi:10.1177/0192512199201002.
16 Ellis, B. (1968). Basic Concepts of Measurement. Cambridge: Cambridge University Press
17 Allan, Pierre, and Cédric Dupont. 1999. "International Relations Theory And Game Theory: Baroque Modelling Choices And Empirical Robustness". International Political Science Review 20 (1): 23-47. doi:10.1177/0192512199201002.
18 HARSANYI, JOHN C. 1992. "In Defense Of Game Theory". Rationality And Society 4 (1): 51-61.doi:10.1177/1043463192004001007.
19 Mor, Ben D. 1992. "Nuclear Deterrence Theory: The Search For Credibility. By Robert Powell. Cambridge: Cambridge University Press, 1990. 230P. $47.50.". American Political Science Review 86 (1): 293-294. doi:10.2307/1964119
20 Tasci, Deniz. 2020. "GAME THEORY: Importance, Applications and Contributions In International Relations". Researchgate.Net
21 See Langlois, Catherine C., and Jean-Pierre P. Langlois. 2009. "Does Attrition Behavior Help Explain The Duration Of Interstate Wars? A Game Theoretic and Empirical Analysis". International Studies Quarterly 53 (4): 1051-1073. doi:10.1111/j.1468-2478.2009.00568.x.
22 Kydd, Andrew. 1997. "Game Theory and The Spiral Model". World Politics 49 (3): 371-400. doi:10.1353/wp.1997.0012.
23 Conrad, Courtenay, and Emily Hencken Ritter. 2013. “Treaties, Tenure, and Torture: The Conflicting Domestic Effects of International Law.” The Journal of Politics 75 (2): 397–409
24 Maoz, Zeev. 1985. "Decision-Theoretic and Game-Theoretic Models of International Conflict", in Luterbacher, Urs and Ward, Michael D. (eds.), Dynamic Models of International Conflict, Lynne Rienner Publishers: Boulder, CO
25 HARSANYI, JOHN C. 1968. “Games with Incomplete Information Played by "Bayesian" Players. Management Science (A).159:320. 486.
26 Brams, Steven J. 2000. "Game Theory: Pitfalls and Opportunities in Applying It To International Relations". Peace Economics, Peace Science and Public Policy 6 (2). doi:10.2202/1554-8597.1032.
References:
Allan, Pierre, and Cédric Dupont. 1999. "International Relations Theory And Game Theory: Baroque Modeling Choices And Empirical Robustness". International Political Science Review 20 (1): 23-47. doi:10.1177/0192512199201002.
Alzawahreh, Abdallah. (2021). Prisoner 's Dilemma Theory in International Relations:A Theoretical and Practical Study on Saudi-Iranian Relations. 17. 30-34. 10.3968/12291.
Amartya, Sen. 1992 "Rational Fools: A Critique of the Behavioural Foundations of Economic Theory."
Barkin, J. Samuel. 2015. "On The Heuristic Use Of Formal Models In International Relations Theory". International Studies Review, n/a-n/a. doi:10.1111/misr.12253.
Bennett, Peter G. 1995. "Modelling Decisions In International Relations: Game Theory And Beyond". Mershon International Studies Review 39 (1): 19. doi:10.2307/222691.
Binmore, K. G. 2008. Game Theory. Oxford: Oxford University Press.
Brams, Steven J. 2000. "Game Theory: Pitfalls And Opportunities In Applying It To International Relations". Peace Economics, Peace Science And Public Policy 6 (2).doi:10.2202/1554-8597.1032.
Bueno de Mesquita. 2002. Accomplishments and Limitations of a Game-Theoretic Approach to International Relations
Correa, Hector. 2022. "Game Theory As An Instrument For The Analysis Of International Relations". Ritsumei.Ac.Jp. Accessed March 8.
Ellis, B. (1968). Basic Concepts of Measurement. Cambridge: Cambridge University Press
Friedman, Jeffrey. 1996. Introduction: Economic Approaches To Politics. In The Rational Choice Controversy. New Haven: Yale University Press.
Gibbons, Robert. 1997. "An Introduction To Applicable Game Theory". Journal Of Economic Perspectives 11 (1): 127-149. doi:10.1257/jep.11.1.127.
Harsanyi, John C.1992. "In Defense Of Game Theory". Rationality And Society 4 (1): 51-61. doi:10.1177/1043463192004001007.
Harsanyi, John C.1968. “Games with Incomplete Information Played by "Bayesian" Players. Management Science (A)” 159:320. 486.
Iklé, Fred Charles, and Nathan Leites. 1962. "Political Negotiation As A Process Of Modifying Utilities". Journal Of Conflict Resolution 6 (1): 19-28.doi:10.1177/002200276200600103.
Langlois, Catherine C., and Jean-Pierre P. Langlois. 1996. "Rationality In International Relations: A Game-Theoretic And Empirical Study Of The U.S.-China Case". World Politics 48 (3): 358-390. doi:10.1353/wp.1996.0012
Langlois, Catherine C., and Jean-Pierre P. Langlois. 2009. "Does Attrition Behavior Help Explain The Duration Of Interstate Wars? A Game Theoretic And Empirical Analysis". International Studies Quarterly 53 (4): 1051-1073. doi:10.1111/j.1468- 2478.2009.00568.x.
Levy, Jack S. 1997. "Prospect Theory, Rational Choice, And International Relations". International Studies Quarterly 41 (1): 87-112. doi:10.1111/0020-8833.00034
Maoz, Zeev. 1985. "Decision-Theoretic and Game-Theoretic Models of International Conflict", in Luterbacher, Urs and Ward, Michael D. (eds.), Dynamic Models of International Conflict, Lynne Rienner Publishers: Boulder, CO
Mor, Ben D. 1992. "Nuclear Deterrence Theory: The Search For Credibility. By Robert Powell. Cambridge: Cambridge University Press, 1990. 230P. $47.50.". American Political Science Review 86 (1): 293-294. doi:10.2307/1964119.
O'Neill. Steven J. Brams and D. Marc Kilgour. 1988. Game Theory and National Security. New York Basil Blackwell
Olson, Mancur, and Richard Zeckhauser. 1966. "An Economic Theory Of Alliances". The Review Of Economics And Statistics 48 (3): 266. doi:10.2307/1927082.
Powell, Robert. 1999. "The Modeling Enterprise And Security Studies". International Security 24 (2): 97-106. doi:10.1162/016228899560176.
Powell, Robert. 1999. In The Shadow Of Power
Quackenbush, Stephen L. and Zagare, Frank C. 2006. “Game Theory: Modelling Interstate
Conflict.” Sterling-Folker. Jennifer (ed.). Making Sense of International Relations Theory (Boulder, CO.: Lynne Rienner, 2006), pp. 98–114
Robert, Axelrod. 1984. The Evolution of Cooperation. New York: Basic Books.
Rubinstein, Ariel. 1991. "Comments On The Interpretation Of Game Theory". Econometrica 59 (4): 909. doi:10.2307/2938166.
Snidal, Duncan. 1985. "The Game Theory Of International Politics". World Politics 38 (1): 25-57. doi:10.2307/2010350.
Tasci, Deniz. 2020. "GAME THEORY: Importance, Applications And Contributions In International Relations". Researchgate.Net.
Tema, Malvina. 2014. "Basic Assumptions In Game Theory And International Relations". International Relations Quarterly 5 (1): 1-4
Wagner, R. Harrison. 1983. "The Theory Of Games And The Problem Of International Cooperation". American Political Science Review 77 (2): 330-346. doi:10.2307/1958919.


